Điểm thi đại học: 05/08/12

Đề thi thử đại học môn hóa 2012 (Chuyên ĐHSP)

Đề thi thử đại học năm 2012 môn vật lý có lời giải của trường THPT chuyên Đại học sư phạm Hà Nội.

Điểm thi đại học năm 2012

Đề thi thử môn hóa lần 1

Đề thi thử môn hóa lần 2

Đề thi thử môn hóa lần 3

Đề thi thử môn hóa lần 4

Đề thi thử môn hóa lần 5

Đề thi thử môn toán đại học năm 2012 (đề 1)

Đề thi thử môn toán vào đại học khối D năm 2012 của trường THPT Phan Đình Phùng- Hà Nội.

Đề thi: Tải tại đây

Đáp án chi tiết tại đây

Điểm thi đại học năm 2012

Đề thi thử môn toán 2012 (Đề số 4- Toán học tuổi trẻ)

Mời các sĩ tử tham gia thi thử Đại học- Cao đẳng năm 2012 trong chuỗi đề thi thử trên tạp chí Toán học tuổi trẻ

Đề thi thử số 4 (Đáp án sẽ được cập nhật sớm nhất):

PHẦN CHUNG

CÂU I. Cho hàm số: 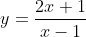$y=\frac{2x+1}{x-1}$ (C)

1) Khảo sát và vẽ đồ thị hàm số (C)

2) Gọi M là một điểm nằm trên (C) có hoành độ lớn hơn 1, I là giao điểm hai đường tiệm cận. Tiếp tuyến với (C) tại M, cắt tiệm cận đứng tại A, cắt tiệm cận ngang tại B. Tính diện tích tam giác IAB.

CÂU II.

1)Giải phương trình:

$\frac{1+\cot2x.\cot x}{\cos^2x}+1=6(sin^4x+\cos^4x)$

2)Giải phương trình:

$\sqrt{{36x}^{2}-63x+ 27}=15-27x + 2\sqrt{{9x}^{2}-9x+3}$

CÂU III. Tính tích phân

$I = \int\limits_{0}^{2}\frac{x+2}{(x+1)({x}^{2}+2x+4)}dx$

CÂU IV.
Cho hình hộp ABCD.A’B'C’D’. M và N là hai điểm lần lượt thuộc cạnh AB và AD sao cho

$AM=\frac{2}{3}AB$ ; $AN=\frac{3}{4}AD$ .

E và F là hai điểm lần lượt thuộc B’N và A’M sao cho EF song song AC. Hãy xác định tỉ số 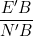$\dfrac{E'B}{N'B}$

CÂU V. Cho x,y là các số thực thỏa mãn 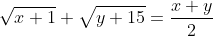$\sqrt{x+1} + \sqrt{y+15} = \frac{x+y}{2}$
Tìm giá trị lớn nhất và nhỏ nhất của

$P= x+y$

PHẦN RIÊNG

A. Theo chương trình chuẩn

CÂU VIa
1)Cho tam giác ABC có AB=3AC . Đường phân giác góc BAC có phương trình là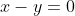 $x-y=0$ , đường cao BH có phương trình là 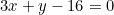$3x+y-16=0$ . Hãy xác định tọa độ A, B, C , biết rằng đường thẳng AB đi qua $M(4;10)$ .

2) Trong không gian cho điểm A(1;0;0) và hai đường thẳng

$\Delta_1:\frac{x-5}{3}=\frac{y-1}{1}=\frac{z-2}{2}$ ; $\Delta_2:\frac{x-5}{1}=\frac{y-1}{1}=\frac{z-3}{3}.$ .

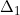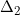Gọi B và C là hai điểm lần lượt thuộc $\Delta _1$ và $\Delta _2$ sao cho A, B, C thẳng hàng. Tìm điểm M trên trục tung sao cho diện tich tam giác BMC bằng 3.

CÂU VIIa. Tìm m để phương trình có nghiệm

$12\sqrt{4+x-3{x}^{2}}=3x-24+m(3\sqrt{x+1}+2\sqrt{4-3x)}$

Theo chương trình nâng cao

CÂU VI.b
1) Trong hệ tọa độ Oxy cho elip(E):

$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{4}=1$

M và N là hai điểm trên (E) sao cho tam giác OMN vuông tai O (gốc tọa độ). H là hình chiếu O lên MN. Chứng minh rằng khi M, N thay đổi thì H chạy trên đường tròn cố định. Viết phương trình đường tròn đó.
2) Có 20 quyển sách gồm 5 toán, 7 lí, 8 Hóa , các sách cùng loại giống nhau. Số sách này chia đều cho 10 học sinh, mỗi học sinh chỉ nhận được 2 cuốn khác loại. Hạnh và Vân là 2 bạn trong 10 bạn đó. Tính xác suất để 2 cuốn sách mà Hạnh nhận được giống Vân.

CÂU VII.b
Giải hệ phương trình:

$\begin{cases}\frac{\log_2x}{1+\log_2^2x}+\frac{\log_2y}{1+\log_2^2y}&=\frac{9}{10}\\(1+\log_x2.\log_y2)\log_2(xy)&=\frac{9}{2}.\end{cases}$

Các bài liên quan

Đề thi thử môn toán 2012 (Đề số 5- Toán học tuổi trẻ)

Mời các sĩ tử tham gia thi thử Đại học- Cao đẳng năm 2012 trong chuỗi đề thi thử trên tạp chí Toán học tuổi trẻ

Đề thi thử số 5 (Đáp án sẽ được cập nhật sớm nhất):

Câu I:Cho hàm số $y=\frac{x+1}{x-1}(C)$
1,Khảo sát sự biến thiên và vẽ đồ thị (C)

của hàm số.
2,Tìm những điểm trên trục tung để từ đó kẻ được đúng một tỉếp tuyến với (C)

Câu II:
1,Giải phương trình:
$\frac{1}{2cot^2x+1}+\frac{1}{2tan^2x+1}=\frac{15cos4x}{8+sin^22x}$
2, Giải hệ phương trình:
$\left\{\begin{matrix} \frac{x^2}{(y+1)^2}+\frac{y^2}{(x+1)^2}=\frac{1}{2} & \\ 3xy=x+y+1& \end{matrix}\right.$